PRIMER PARCIAL SEGUNDO QUIMESTRE FUNCIONES CONCEPTOS BÁSICOS Y FUNCIÓN AFÍN
FUNCIONES
CONCEPTOS BASICOS


Ejemplos:1Representar gráficamente y = 2x + 3



CONCEPTOS BASICOS
En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio ) y otro conjunto de elementos Y (llamado codominio ) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito ).
En lenguaje cotidiano o más simple, diremos que las funciones matemáticas equivalen al proceso lógico común que se expresa como “depende de”.
Las funciones matemáticas pueden referirse a situaciones cotidianas, tales como: el costo de una llamada telefónica que depende de su duración, o el costo de enviar una encomienda que depende de su peso.
A modo de ejemplo, ¿cuál sería la regla que relaciona los números de la derecha con los de la izquierda en la siguiente lista?:
1 --------> 1
2 --------> 4
3 --------> 9
4 --------> 16
Los números de la derecha son los cuadrados de los de la izquierda.
La regla es entonces "elevar al cuadrado":
1 --------> 1
2 --------> 4
3 --------> 9
4 --------> 16
x --------> x 2 .
Para referirse a esta regla podemos usar un nombre, que por lo general es la letra f (de función). Entonces, f es la regla "elevar al cuadrado el número".
Usualmente se emplean dos notaciones:
x --------> x 2 o f(x) = x 2 .
Así, f(3) significa aplicar la regla f a 3. Al hacerlo resulta 3 2 = 9.
Entonces f(3) = 9. De igual modo f(2) = 4, f(4) = 16, f(a) = a 2
Con estos ejemplos vamos entendiendo la noción de función: como vemos, todos y cada uno de los elementos del primer conjunto (X) están asociados a uno, y sólo a uno, del segundo conjunto (Y) . Todos y cada uno significa que no puede quedar un elemento en X sin su correspondiente elemento en Y . A uno y sólo a uno significa que a un mismo elemento en X no le pueden corresponder dos elementos distintos en Y .
Ahora podemos enunciar una definición más formal:
Una función ( f) es una regla que asigna a cada elemento x de un conjunto X (dominio) exactamente un elemento, llamado f(x) , de un conjunto Y (codominio) .
Otra definición equivalente es: sean X e Y dos conjuntos. Una función de X en Y es una regla (o un método) que asigna un (y sólo uno) elemento en Y a cada elemento en X .
Usualmente X e Y son conjuntos de números.
Generalizando, si se tiene una función f , definida de un conjunto A en un conjunto B, se anota
f : A -----> B (o, usando X por A e Y por B f : X -----> Y) o f(x) = x
Recordemos de nuevo que el primer conjunto A se conoce como dominio (Dom) de la función y B es el codominio o conjunto de llegada.
f(x) denota la imagen de x bajo f , mientras que x es la preimagen de f(x) .
En el ejemplo 2 anterior el número 3 es la imagen del número 0 bajo f; por su parte, 1 es la preimagen del número 5.
El rango (Rg) o recorrido (Rec) o ámbito (A) es el conjunto de todos los valores posibles de f(x) que se obtienen cuando x varía en todo el dominio de la función.
Ejemplo 3
Suponga que el conjunto A (de salida) es A = {1, 2, 3} y que el conjunto B (de llegada) es B = {0, 4, 6, 8, 10, 12} y que la relación de dependencia o correspondencia entre A y B es "asignar a cada elemento su cuádruplo".
Vamos a examinar si esta relación es una función de A en B y determinaremos dominio y recorrido.
Veamos:
A los elementos 1, 2 y 3 del conjunto A les corresponden, respectivamente, los elementos 4, 8 y 12 del conjunto B. Como a cada elemento de A le corresponde un único elemento de Y, la relación de dependencia es una función (función de A en B).
Dominio = {1, 2, 3} Recorrido = {4, 8, 12}
Notar que el recorrido es un subconjunto del codominio B = {0, 4 , 6, 8 , 10, 12 }
Aquí debemos recordar que toda función es una relación , pero no todas las relaciones son funciones. Como ejemplos de relaciones que son funciones y algunas que no lo son, veamos las siguientes:
Si tenemos los conjuntos
A = {1 ; 2 ; 3 ; 4}, B = {1 ; 2 ; 3 ; 4 ; 5}
Podemos establecer las relaciones
f = { (1 ; 2) ; (2 ; 3) ; (3 ; 4) ; (4 ; 5) }
g = { (1 ; 2) ; (1 ; 3) ; (2 ; 4) ; (3 ; 5) ; (4 ; 5) }
h = { (1 ; 1) ; (2 ; 2) ; (3 ; 3) } :
Está claro que f , g y h son relaciones de A en B , pero sólo f es una función (todos los elementos del conjunto A tiene su correspondiente elemento en b); g no es función ya que (1 ; 2) y (1 ; 3) repiten un elemento del dominio (el 1). Tampoco h es una función ya que Dom ( h ) = {1 ; 2 ; 3} ≠ A (falta el 4).
Ejemplo 4
Sea X = {−4, −1, 0, 4, 9}, Y = {−4,−3, −2, −1, 0, 1, 2, 3, 4} y que la regla de correspondencia es " asignar a cada elemento de X el resultado de extraer su raíz cuadrada".
Vamos a determinar si esta regla constituye función de X en Y.
Veamos:
A simple vista se aprecia que los números 0, 4, 9 tienen imagen en Y ( 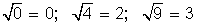 ), pero a los números −4 y −1 no les corresponden elementos en Y. Como existen elementos de X que no se corresponden con elementos de Y, esta relación no es función de X en Y.
), pero a los números −4 y −1 no les corresponden elementos en Y. Como existen elementos de X que no se corresponden con elementos de Y, esta relación no es función de X en Y.
Dominio y rango de una función
Como ya vimos, el dominio de una función es el conjunto de valores para los cuales la función está definida; es decir, son todos los valores que puede tomar la variable independiente (la x) .
Por ejemplo la función f(x) = 3x 2 – 5x está definida para todo número real ( x puede ser cualquier número real). Así el dominio de esta función es el conjunto de todos los números reales.
En cambio, la función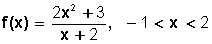 tiene como dominio todos los valores de x para los cuales −1< x < 2, porque aunque pueda tomar cualquier valor real diferente de –2, en su definición determina en qué intervalo está comprendida.
tiene como dominio todos los valores de x para los cuales −1< x < 2, porque aunque pueda tomar cualquier valor real diferente de –2, en su definición determina en qué intervalo está comprendida.
En cambio, la función
Si el dominio no se específica, debe entenderse que el dominio incluye a todos los números reales para los cuales la función tiene sentido.
En el caso de la función 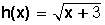 , el dominio de esta función son todos los números reales mayores o iguales a –3, ya que x + 3 debe ser mayor o igual que cero para que exista la raíz cuadrada.
, el dominio de esta función son todos los números reales mayores o iguales a –3, ya que x + 3 debe ser mayor o igual que cero para que exista la raíz cuadrada.
Como resumen, para determinar el dominio de una función, debemos considerar lo siguiente:
Si la función tiene radicales de índice par, el dominio está conformado por todos los números reales para los cuales la cantidad subradical sea mayor o igual a cero.
Si la función es un polinomio; una función de la forma f(x) = a 0 + a 1 x + a 2 x 2 +...+ a n x n (donde a 0 , a 1 , a 2 ,..., a n son constantes y n un entero no negativo), el dominio está conformado por el conjunto de todos los números reales.
Si la función es racional; esto es, si es el cociente de dos polinomios, el dominio está conformado por todos los números reales para los cuales el denominador sea diferente de cero.
El rango ( recorrido o ámbito ) es el conjunto formado por todas las imágenes; es decir, es el conjunto conformado por todos los valores que puede tomar la variable dependiente; estos valores están determinados además, por el dominio de la función.
Ejemplo
Identificar dominio y rango de la función 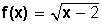
Veamos:
Como la función tiene radicales el dominio está conformado por todos los valores para los cuales x – 2 ≥ 0. Esto es, el dominio de la función incluye todos los reales que son mayores o iguales a 2.
El rango es igual al conjunto de los números reales positivos incluyendo el cero; puesto que al reemplazar los valores del dominio se obtienen únicamente valores positivos bajo la función f .
FUNCIÓN AFIN
a función afín es del tipo:
y = mx + n
m es la pendiente de la recta.
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Dos rectas paralelas tienen la misma pendiente.

n es la ordenada en el origen y nos indica el punto de corte de la recta con el eje de ordenadas.
Su gráfica es una línea recta que no pasa por el origen de coordenadas.

Para representar la función le damos al menos dos valores
Le damos valores a la función
y = 2 · 0 + 3 = 3
y = 2 · 1 + 3 = 5
y = 2 · 2 + 3 = 7
y = 2 · 3 + 3 = 9
y = 2 · 4 + 3 = 11
| x | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| y = 2x | 3 | 5 | 7 | 9 | 11 |

El punto (0, 3) es la ordenada en el origen.
2 y = 2x - 1
| x | y = 2x-1 |
|---|---|
| 0 | -1 |
| 1 | 1 |

2 y = -¾x - 1
| x | y = -¾x-1 |
|---|---|
| 0 | -1 |
| 4 | -4 |

Una función afín es una función que, en cualquier valor x definido en ℝ (la escala de los números reales), asocia el número ax + b, siendo «a» y «b» números relativos.
Representamos esta función mediante la ecuación siguiente: f(x): ax + b of(x) = ax + b.
El número «b» debe ser diferente a 0. ¿Por qué? Porque si b = 0, entonces tenemos que f(x) = ax y entonces hablamos de una función afín lineal.
Si «a» es igual a cero, entonces decimos que la función f(x) = b es constante (y afín); de hecho, todos los puntos de la misma línea tienen el mismo eje de ordenadas (b) y la curva será paralela al eje de abscisas.
Estas son las dos particulares que tendrás que tener en cuenta con la función afín.
El valor «b» representa, en una representación gráfica, la ordenada en el origen: es el punto donde la curva pasa por el eje de ordenadas (y) en su distancia desde el origen (0).
La variable «a», denominada «coeficiente de dirección», hace referencia al grado de la pendiente de la curva, calculable a partir del eje de abscisas (x) en la gráfica.
Cuanto mayor sea el número «a», mayor será la pendiente de la curva, que podrá ser positiva o negativa.
Para causar una buena impresión en los ejercicios de representación gráfica matemática en la prueba de acceso a la Universidad, podrás escribir que la recta de f(x) mide la tasa de aumento de las ordenadas por unidad de abscisas.
Por lo tanto, una función afín es un conjunto de valores que resuelve la ecuación y = ax + b, en el intervalo dado, y cuya representación gráfica tomará la forma de una recta oblicua, creciente o decreciente.
Entonces, debemos leer que «f» es la función que en el número «x» coincide con el número «ax + b»: «x» es el antecedente, «ax + b», la imagen de «x» en el intervalo. El resultado escrito es f(x) = ax + b.
Por ejemplo si f(x) = 3x, obtendremos una recta, denominada d1, creciente, que corta el eje de ordenadas en el punto 0. Si f(x) = -x, entonces tendremos la recta d2, que será decreciente.
Otra peculiaridad que deberás tener en cuenta es que si f(x) = -5, entonces la línea será constante y cruzará el eje en el punto -5.
Para calcular la imagen de un «x» real, bastará con multiplicar «x» por el coeficiente «a» y sumar la constante «b». Entonces, podremos comenzar a dibujar la recta en la gráfica. Aborda estas nociones durante las clases de matemáticas con tu profesor particular.
.gif)
Comentarios
Publicar un comentario