Limites matemáticos

LIMITES MATEMÁTICOS

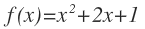
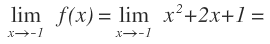
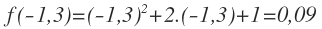
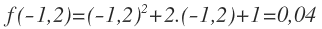
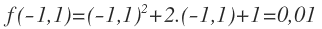
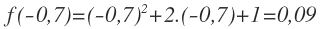
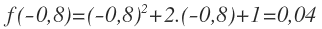
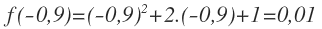
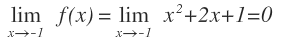
El término que ahora vamos a analizar es interesante recalcar que está formado por la unión de dos vocablos que tienen su origen etimológico en lenguas antiguas. Así, límites procede de la palabra latina limes, que es el genitivo de limitis que puede traducirse como borde o frontera de algo.

Por su parte, matemáticos es una palabra que tiene su citado origen en el griego y concretamente en el término mathema. Este puede definirse como el estudio de un tema o asunto determinado.

La división que marca una separación entre dos regiones se conoce como límite. Este término también se utiliza para nombrar a una restricción o limitación, al extremo que se puede alcanzar desde el aspecto físico y al extremo a que llega un periodo temporal.

Para la matemática, un límite es una magnitud a la que se acercan progresivamente los términos de una secuencia infinita de magnitudes. Un límite matemático, por lo tanto, expresa la tendencia de una función o de una sucesión mientras sus parámetros se aproximan a un cierto valor.

Una definición informal del límite matemático indica que el límite de una función f(x) es T cuando x tiende a s, siempre que se puede hallar para cada ocasión un x cerca de s de manera tal que el valor de f(x) sea tan cercano a T como se pretenda.

No obstante, además del límite citado, no podemos obviar que existen otros muy importantes en el ámbito de las Matemáticas. Así, también se puede hablar del límite de una sucesión que puede ser existente o único y divergente, en el caso de que los términos de aquella no converjan en ningún punto.

De la misma manera, también hay que hablar de otra serie de límites matemáticos tales como el límite de una sucesión de conjuntos o el de espacios topológicos. Entre estos últimos están los que hacen referencia a los filtros o a las redes.

Finalmente tampoco podemos pasar por alto la existencia de lo que se conoce como Límite de Banach. Este último, que recibe el nombre del matemático polaco Stefan Banach, es aquel que gira entorno a lo que se conoce como espacio de Banach. Este es una pieza fundamental dentro de lo que es el análisis funcional y puede definirse como el espacio donde están funciones que cuentan con una dimensión infinita.

Al igual que otros conceptos matemáticos, los límites cumplen con diversas propiedades generales que ayudan a simplificar los cálculos. Sin embargo, puede resultar muy difícil comprender esta idea ya que se trata de un concepto abstracto.

En matemática, la noción está vinculada con la variación de los valores que toman las funciones o sucesiones y con la idea de aproximación entre números. Esta herramienta ayuda a estudiar el comportamiento de la función o de la sucesión cuando se acercan a un punto dado.

La definición formal del límite matemático fue desarrollada por diversos teóricos de todo el mundo a lo largo de los años, con trabajos que constituyeron la base del cálculo infinitesimal.

DEFINICIÓN DE LIMITACIÓN 

el latín limitatio, limitación es la acción y efecto de limitar o limitarse. El verbo limitar refiere a poner límites a algo, mientras que la noción de límite está vinculada a una línea que separa dos territorios, al extremo a que llega un determinado tiempo, al extremo que puede alcanzar lo anímico y lo físico o a una restricción.

Limitación, por lo tanto, puede utilizarse como sinónimo de límite en ciertos contextos. Por ejemplo: “El presupuesto que tenemos es una limitación para reforzar el equipo, pero haremos lo posible para sumar jugadores de jerarquía”, “Si contrata este paquete, podrá utilizar el servicio sin ningún tipo de limitación”, “La Justicia impuso limitaciones al uso del espacio público para evitar conflictos entre los vecinos”, “En Argentina, se conoce como tenedor libre a los restaurantes que permiten comer todo lo que uno desea, sin ninguna limitación y por un precio fijo”.

 Una limitación puede ser cualquier tipo de restricción. La limitación de velocidad indica la velocidad máxima permitida en ciertos caminos. Si la limitación de velocidad en una carretera provincial es de 90 kilómetros por hora, los conductores no están habilitados para exceder dicha velocidad. Por lo tanto, si lo hacen, pueden ser multados o sancionados.

La limitación de tráfico, por otra parte, está vinculada a la prohibición de circulación de vehículos en determinados horarios o lugares. Estas limitaciones son habituales para la protección de ciertos entornos naturales, de manera tal de reducir los niveles de contaminación. Un ejemplo de limitación de tráfico tiene lugar en los parques nacionales en los que se permite el ingreso de sólo cien automóviles por día.

Entendido de forma simbólica, los seres vivos tenemos ciertas habilidades, que se ven restringidas por nuestras limitaciones. Por ejemplo, no todas las personas que tienen talento para tocar el piano pueden llegar a ser grandes músicos, dado que existe una serie de requisitos que sólo unos pocos son capaces de superar; en otras palabras, no tener oído absoluto, no poseer destrezas similares en ambas manos, o bien sufrir alguna enfermedad en los huesos o tener una cierta deformidad física pueden representar limitaciones, dependiendo de los objetivos.

Reconocer nuestras limitaciones es muy importante para desarrollarnos como personas, tanto en el ámbito profesional como en el emocional. Tener una limitación es natural: no existe ser vivo cuyas habilidades sean infinitas. Por lo tanto, nadie debería sentirse avergonzado de estos muros que marcan hasta dónde podemos llegar; por el contrario, descubrirlos y aceptarlos es la clave para aprovechar nuestro potencial.

A menudo se lee en las biografías de los grandes artistas que desde pequeños supieron qué querían ser de mayores; cantantes que balbuceaban melodías complejas desde la cuna, pianistas que con tan sólo tres años se abalanzaron sobre el primer piano que conocieron o dibujantes que sorprendieron a sus familias con sus primeros bocetos infantiles, son algunos de los ejemplos de personas que tuvieron claras sus vocaciones sin necesidad de probar otros campos.

Sin embargo, por una combinación de diferentes factores, hay quienes necesitan recorrer más de un camino hasta dar con eso que les apasiona, con esa disciplina o actividad sin la cual no pueden alcanzar la felicidad. Para dar con esa revelación, es esencial toparse con las propias limitaciones, reconocerlas como tales, y cambiar de rumbo, sin permitir que se conviertan en frustraciones.

A veces, por otro lado, una limitación puede ser un bloqueo pasajero o circunstancial, que responda a un trauma posible de superar. Diversos motivos pueden llevarnos a sentir que no somos capaces de enfrentar ciertas situaciones, aunque las razones no puedan ser apreciadas por terceros; en esos casos, una adecuada introspección y un constante trabajo de análisis pueden ser de gran ayuda.

No hay que confundir el límite de una función con el valor de una función en punto, que es el valor que tiene la función justo en ese punto. Mucho cuidado porque pueden no coincidir (lo veremos más adelante).

Vamos a verlo con un ejemplo.

¿Cuál es el límite de la siguiente función:

cuando x tiende a -1?

El límite de la función cuando x tiende a -1 se escribe:

Para que entiendas como el valor de la función se va a aproximando a un valor determinado, mientras que x va tendiendo a -1, vamos a ir viendo cuál es el valor de la función para los puntos que próximos a -1 y cada vez nos vamos a ir acercando más a -1.

Primero nos vamos a ir acercando cada vez más a -1 por la izquierda a ver qué pasa.

Cuando x=-1,3, el valor de la función es:

Cuando x=-1,2, el valor de la función es:

Cuando x=-1,1, el valor de la función es:

Si te das cuenta, conforme nos vamos acercando a -1, el valor de la función se va aproximando a 0.

Vamos hacer lo mismo ahora, pero acercándonos al 1 por la derecha.

Cuando x=-0,7, el valor de la función es:

Cuando x=-0,8, el valor de la función es:

Cuando x=-0,9, el valor de la función es:

Como puedes observar, conforme nos vamos acercando a x=-1 por la derecha, la función se va aproximando cada vez más a 0.

Si lo vemos en una gráficamente, vemos como la gráfica de la función se aproxima al punto 0 en el eje y, cuando los valores de x se van a aproximando al punto -1 en el eje x:

Por tanto, el límite de la función cuando x tiende a -1 es igual a 0:

Para resolver un límite no es necesario realizar este procedimiento que acabamos de hacer. Tan solo lo he hecho para que fueras viendo cómo poco a poco el valor de la función se va aproximando a un punto.

Resolver el límite de esa función es mucho más sencillo y es lo que te voy a explicar en el siguiente apartado.