2do Parcial 1er Quimestre Operaciones con radicales

A) Suma de radicales.

LA regla general es que solo podemos operar con radicales semejantes, vamos a diferenciarlos:

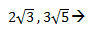 No son semejantes, ya que tienen distintos coeficientes

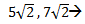 Son semejantes, ya que poseen el mismo coeficiente, ese raíz de dos.

**Nota: El coeficiente debe ser el mismo tanto en número como en índice, es decir, no podríamos operar con un raíz cúbica y una raíz cuadrada.

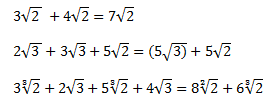
Como podéis observar los radicales se suman como si fuesen equis e íes, casa cosa con su nombre, los cuadrados con los cuadrados, y los cubos con los cubos, y así sucesivamente.

**Nota: Muy importante, no es lo mismo:

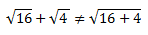
Ya que en el primer caso, nos daría 4+2= 6 y en el segundo raíz de 20.

B) Resta de radicales.

Si habéis entendido el apartado anterior, este os será fácil, ya que es lo mismo, pero restando, como si fuesen números normales, siempre respetando los coeficientes, por supuesto. Ejemplo:

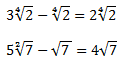
Aquí tengo que aclararos varias cosas: si no aparece ningún número
delante del radical, presuponemos siempre que es 1, y os podéis encontrar con casos en los que el índice de la raíz cuadrada (ese dos pequeñito que sale arriba) os aparezca o no, si no tiene índice
se presupone siempre que es cuadrada, ya que es el mínimo índice que tienen los radicales.

C) Multiplicación de radicales.

Como antes, para poder multiplicar, los radicales han de ser del mismo orden, es decir, semejantes.

Multiplicaremos los radicales y los números que los multiplican por separado. Ejemplo:

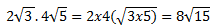
En este caso sí da lo mismo multiplicar lo de dentro que hacerlo por separado, pero solo en el caso de la multiplicación.

D) División de radicales.

Lo mismo que explicamos en la multiplicación pasa en la división, el proceso es exactamente el mismo, realizaremos dos divisiones por separado, las de los números enteros por un lado y las de los radicales por el otro, siempre teniendo en cuenta si son semejantes, esto quiere decir, que no podríamos «disminuir» una raíz cubica con una cuadrada. Ejemplo:

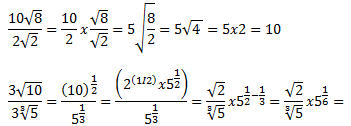
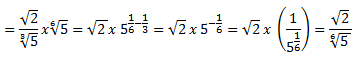
En el segundo caso, al tener distintos grados los radicales, lo único que hemos podido hacer es intentar simplificar un poco el cociente, dividiendo los números enteros y poniendo los radicales en forma de potencias, para observar que solo podíamos operar con la de base 5, desarrollando las diversas potencias que me fui encontrando, hasta llegar a 5 elevado a -1/6, que lo podemos poner positivo pasando a dividir ese exponente.

Para resumir, siempre que veáis que algo dentro de la raíz tiene factores comunes, simplificad.