SISTEMA DE ECUACIONES SEMANA DEL 6/05/2019 AL 10/05/2019
SISTEMA DE ECUACIONES LINEALES
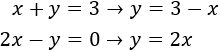
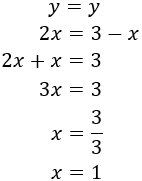
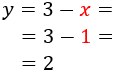
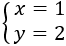
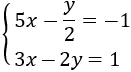
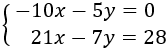
Un sistema de ecuaciones lineales es un conjunto de ecuaciones (lineales) que tienen más de una incógnita. Las incógnitas aparecen en varias de las ecuaciones, pero no necesariamente en todas. Lo que hacen estas ecuaciones es relacionar las incógnitas entre sí.
Ejemplo de un sistema:
Resolver un sistema de ecuaciones consiste en encontrar el valor de cada incógnita para que se cumplan todas las ecuaciones del sistema
los métodosque describimos a continuación, que se basan en la obtención de una ecuación de primer grado.
- Método de sustitución: consiste en despejar o aislar una de las incógnitas (por ejemplo, ) y sustituir su expresión en la otra ecuación. De este modo, obtendremos una ecuación de primer grado con la otra incógnita, . Una vez resuelta, calculamos el valor de sustituyendo el valor de que ya conocemos.
- Método de reducción: consiste en operar entre las ecuaciones como, por ejemplo, sumar o restar ambas ecuaciones, de modo que una de las incógnitas desaparezca. Así, obtenemos una ecuación con una sola incógnita.
- Método de igualación: consiste en aislar en ambas ecuaciones la misma incógnita para poder igualar las expresiones, obteniendo así una ecuación con una sola incógnita.
Método de igualación
Despejamos en ambas ecuaciones la
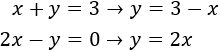
Como , igualamos las expresiones y resolvemos la ecuación:
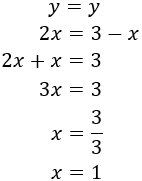
Ahora, sustituimos el valor de la incógnita en la primera de las ecuaciones anteriores para calcular :
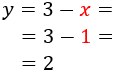
Por tanto, la solución del sistema es
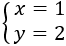
Método de sustitución:
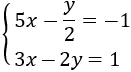
Despejamos en la segunda ecuación la :
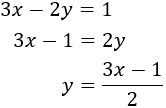 Sustituimos la expresión obtenida en la primera ecuación y la resolvemos:
Sustituimos la expresión obtenida en la primera ecuación y la resolvemos:
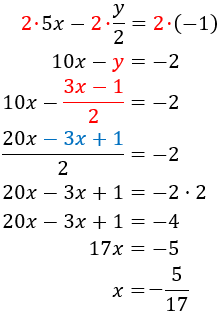 Como ya conocemos , calculamos sustituyendo en alguna de las ecuaciones anteriores:
Como ya conocemos , calculamos sustituyendo en alguna de las ecuaciones anteriores:
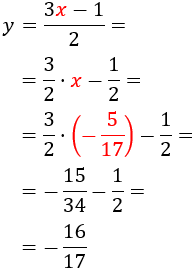 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
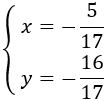
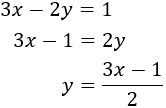
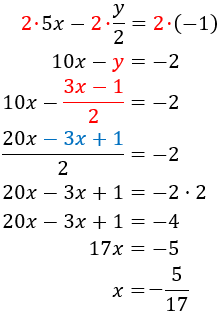
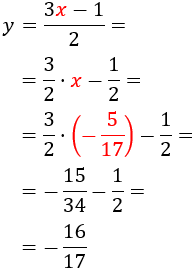
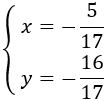
Método de reducción:
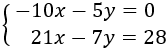
Multiplicamos la primera ecuación por la fracción 1/5 y la segunda por la fracción 1/7:
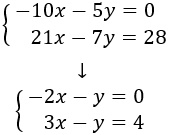 De este modo, evitamos coeficientes altos que complican las operaciones.
De este modo, evitamos coeficientes altos que complican las operaciones.
Ahora, multiplicamos la primera ecuación por 3, la segunda por 2 y las sumamos:
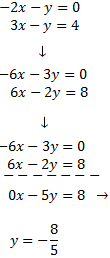 Sustituimos el valor de en la primera ecuación y la resolvemos:
Sustituimos el valor de en la primera ecuación y la resolvemos:
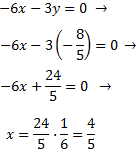 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
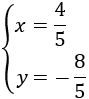
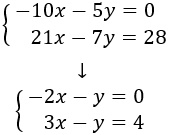
Ahora, multiplicamos la primera ecuación por 3, la segunda por 2 y las sumamos:
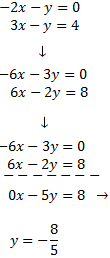
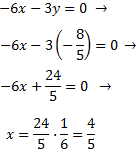
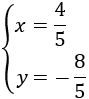
TAREA # 1
RESOLVER LAS SIGUIENTES ECUACIONES POR LOS MÉTODOS ESTUDIADOS


.gif)
Comentarios
Publicar un comentario